Fill the grid using the digits 1-9 four times each. No row or column can contain the same digit more than once. The total of each row and column is provided, as well as clues to the numbers forming the highlighted diagonals (running from bottom left to top right).
Attribution: PUZZLEBOMB.co.uk. Puzzles by @stecks & @apaultaylor.
Solution:
Solving Path
8, 3, the roman numerals and the fahrenheit value in a classic novel (451) are given.
Only 3^5-33 and 3^6-33 are 3 digits, but 3^5-33 contains an invalid zero, therefore it must be 696.
Going through all 4-digit multiples of 487, only 1461 and 5357 come into question using standard scanning. 5357 would force the rest of C5 to sum to 5, which is impossible, therefore it must be 1461.
The multiple of 11 must be 77, all other values produce duplicated digits in the same row/column.
The multiple of nine must be at least 63 to satisfy C6's sum (and can't start with 4/5), 72 would make R7's sum impossible, all other multiples duplicate digits.
The rest of the solving consists of filling in givens and going through the sums and their possible combinations of digits (keeping the max count of 4 in mind)
Gave it a try in "hard mode", where the two knowledge-ish diagonals (MCCCXCVIII and Fahrenheit) are not used in the solving process. It turns out that it is indeed possible to find the unique solution by hand this way.
Solving process:
First, R1 and C8 are trivial. Three-digit "Power of 3 minus 33" has a unique solution of 729 - 33 = 696, because 243 - 33 has a zero.
R8 and C1 have a single possible set of digits, since a 8-cell group has the sum of 45 minus the missing digit. R6 contains 1 through 6, since 21 is the smallest possible sum of 6 numbers.
Now look at "multiple of 11". It indicates that the two cells are equal. With a quick case bashing, it can be found that the diagonal has two 7s, and no other digits work.
In C2, the two missing digits must sum to 8. Such pairs are (1,7), (2,6), and (3,5). Since both 7 and 5 already appear on the column, the missing digits are (2,6).
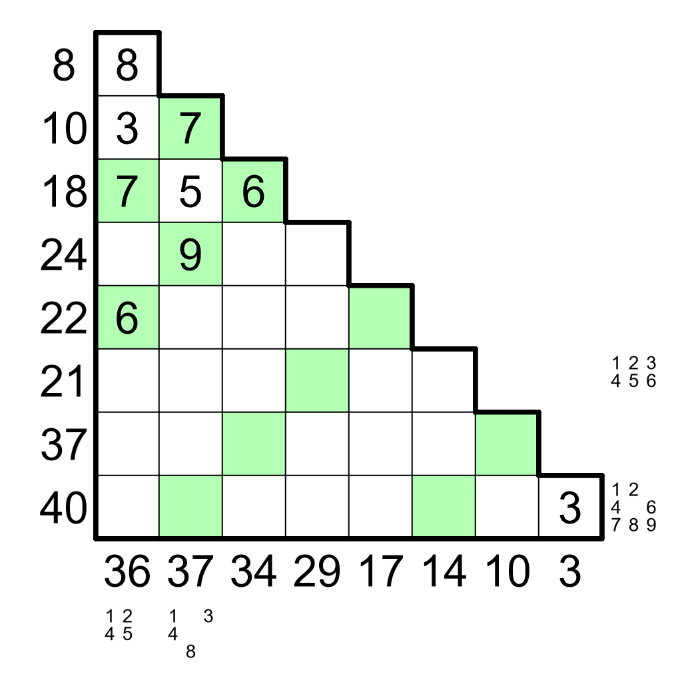
R7 has the same sum as C2. Now focus on the digit 6. Two 6s are already placed, and two others must appear on R6 and R8, so R7 cannot contain a 6. This locks its set of digits.
Counting all other digits, we can find that two more 2s and one more of each of 1, 4, 5, 8, 9 must appear on the remaining cells of R4 and R5. So both R4 and R5 contain a 2, and the five other digits are distributed between the two. The sum of three missing cells on R4 is 15, which minus 2 is 13. 4+9 is not possible since R4 already contains a 9, so the other two digits are 5 and 8.
Now look at the suspicious "multiple of 487". There are 18 4-digit multiples of 487, but there is only one that satisfies all the row/column candidates: 1461. Then C2 is easily fully solved.
Using C7 sum and the "multiple of 9" clue, it can be found that R8C7 can only be either 7 or 9. If it is 9, R7C7 = 1 and R8C6 = 8, which forces R7C6 to be 5, but then no number can go to R7C1. Therefore, R8C7 = 7. Then there is only one way to fill C6.
The four 2s are still not placed, which means that all 4 columns contain a 2. Subtracting it, the 3-cell sum of C3 is 22, and that of C4 is 21. Since 7 and 6 are all used up, the only possibilities are 22 = 5 + 8 + 9 and 21 = 4 + 8 + 9. This also fixes the C5 set.
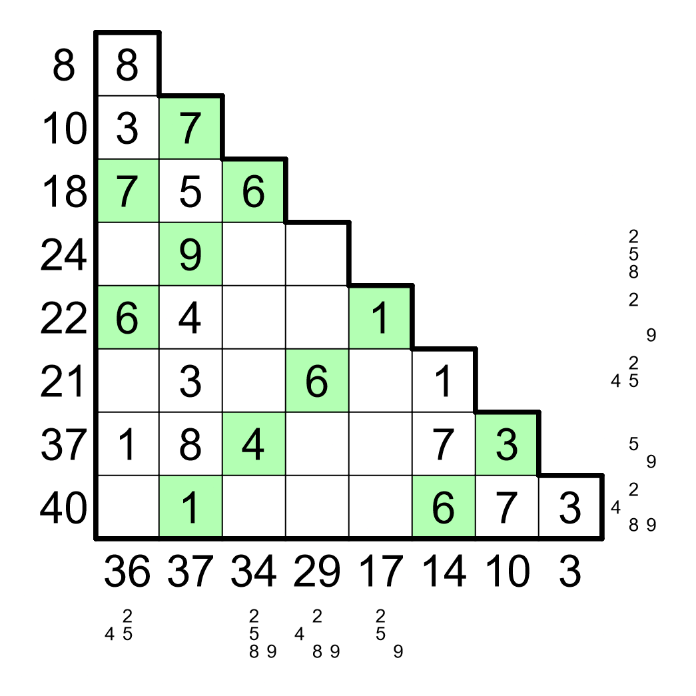
The rest is simple sudoku-style deduction, which gives the final answer:
